Resuelva eficientemente el problema del ortocentro del triángulo
Supongamos que las tres alturas de ⊿ABC son AD, BE y CF, entre las cuales D, E y F son los pies verticales, el centro vertical es H y los lados opuestos de los ángulos A, B y C son a, byc respectivamente
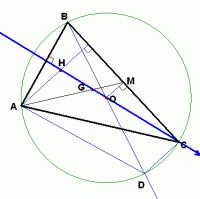
1. El centro perpendicular de un triángulo rectángulo está dentro del triángulo; el centro perpendicular de un triángulo rectángulo está en el vértice del ángulo recto y el centro perpendicular de un triángulo obtuso; triángulo.
2. El centro perpendicular de un triángulo es el incentro de su triángulo perpendicular; en otras palabras, el incentro de un triángulo es el centro perpendicular de su triángulo paracentro; 3. Los puntos de simetría del centro vertical H con respecto a los tres lados están todos en el círculo circunscrito de △ABC.
4. En △ABC, hay seis grupos de cuatro puntos cocirculando, y hay tres grupos (cuatro en cada grupo) de triángulos rectángulos similares, y AH·HD=BH·HE=CH·HF.
5. Cualquier punto entre los cuatro puntos H, A, B y C es el ortocentro del triángulo con los tres puntos restantes como vértices (y esos cuatro puntos se denominan grupo de ortocentros).
6. Los círculos circunscritos de △ABC, △ABH, △BCH y △ACH son círculos iguales.
7. En un triángulo no rectángulo, si la recta que pasa por H corta las rectas AB y AC en P y Q respectivamente, entonces AB/AP·tanB+AC/AQ·tanC=tanA+tanB+tanC. .
8. La distancia desde cualquier vértice de un triángulo al centro vertical es igual al doble de la distancia desde el circuncentro al lado opuesto.
9. Supongamos que O y H son el circuncentro y el ortocentro de △ABC respectivamente, entonces ∠BAO=∠HAC, ∠ABH=∠OBC, ∠BCO=∠HCA.
10. La distancia total desde el ortocentro de un triángulo acutángulo hasta sus tres vértices es igual al doble de la suma de los radios de sus círculos inscritos y circunscritos.
11. El centro perpendicular de un triángulo acutángulo es el incentro del triángulo perpendicular entre los triángulos inscritos del triángulo acutángulo (el vértice está en el lado del triángulo original), el perímetro de la perpendicular; El triángulo es el más corto.
12. Teorema de Simson (línea de Simson): Una condición necesaria y suficiente para la colinealidad de los catetos verticales de las perpendiculares trazadas desde un punto a los tres lados del triángulo es que el punto caiga sobre la circunferencia circunscrita del triángulo.
13 Supongamos que hay un punto P dentro del ángulo agudo ⊿ABC, entonces la condición necesaria y suficiente para que P sea el centro vertical es PB*PC*BC+PB*PA*AB+PA*PC*AC=. AB*BC*CA.
