El efecto Doppler (o desplazamiento Doppler), llamado así por el físico austriaco Christian Doppler, quien lo propuso en Praga en 1842, es el efecto de una onda (u otra onda) cuando un observador se mueve en relación con su fuente. Eventos periódicos. ) cambios de frecuencia. Este sonido se escucha comúnmente cuando los vehículos que hacen sonar sus sirenas o bocinas se acercan, pasan y se alejan del observador. En comparación con la frecuencia de transmisión, la frecuencia de recepción es mayor durante la aproximación, igual durante los momentos de paso y menor durante la retirada.

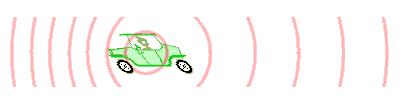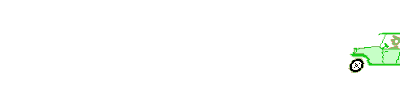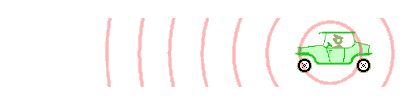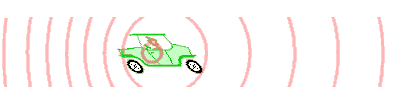
La longitud de onda detrás del efecto Doppler：
Mover la longitud de onda detrás de la fuente de luz：
λ_b = (V-u_s) / f₀
dónde，
λ_f = Mover la longitud de onda detrás de la fuente de luz
v = Velocidad de onda
u_s = velocidad de fuente
f₀ = frecuencia fuente。

¿Necesita comprender el concepto de retraso de longitud de onda en el efecto Doppler? ¡Esta página le brinda la explicación detallada! Explore la fórmula λ' = λ * (1 + v / v_s), donde λ' representa la longitud de onda percibida, λ la longitud de onda original, v la velocidad de la fuente de onda y v_s la velocidad del observador. Además, descubra:

• Fundamentos del efecto Doppler: Aprenda sobre la definición del efecto Doppler, los factores que lo influencian y las aplicaciones prácticas en diversos campos.
• Interpretación del retraso de longitud de onda: Analice cómo el retraso de longitud de onda se relaciona con la dirección del movimiento de la fuente de onda y del observador.
• Cálculos del retraso de longitud de onda: Practique la aplicación de la fórmula λ' = λ * (1 + v / v_s) para resolver problemas relacionados con el retraso de longitud de onda en el efecto Doppler.
• Visualizaciones del retraso de longitud de onda: Observe cómo el retraso de longitud de onda varía en función de la velocidad de la fuente de onda y del observador utilizando gráficos y diagramas.
• Ejemplos del retraso de longitud de onda: Explore casos prácticos del retraso de longitud de onda en diferentes contextos, como el radar, la astronomía y la acústica.