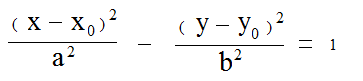La hipérbola se refiere a la trayectoria de un punto donde el valor absoluto de la diferencia entre la distancia a dos puntos fijos en el plano es un valor fijo. También se puede definir como la relación entre la distancia de un punto fijo a un. línea recta fija es mayor que 1. El lugar geométrico de un punto constante. Una hipérbola es un tipo de sección cónica, que es la intersección de una superficie de cono y un plano. Hipérbola a²+b²=c²

Calculadora de ecuaciones de hipérbola

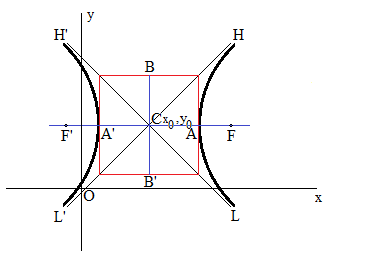
Enfoque hiperbólico eje F X=  x₀ + √(a² + b²)

Enfoque hiperbólico eje F Y=  y₀

Enfoque hiperbólico F' eje X  =  x₀ - √(a^{2 + b2)}

Enfoque hiperbólico F' eje X  =  y₀

Asíntota H'L: y=(b/a)x + y₀ - (b/a)x₀

Asíntota LH': y=(-b/a)x + y₀ + (b/a)x₀

excentricidad hiperbólica=  √(a² + b²)  / a